-
Par topos le 23 Novembre 2009 à 10:37
La meilleure façon de lutter contre la tentation-Badiou, c'est d'en revenir aux fondations de la ligne rationaliste : Platon bien sûr, mais surtout Descartes, Malebranche, Spinoza , expliqués par Brunschvicg.
Descartes a brillamment démontré que l'Infini est D-ieu, qu'il n'y a donc qu'un Infini, qui ne saurait être l'infini, ou les infinis, mathématiques. (On emploie la notation "D-ieu", à la manière des juifs croyants, pour désigner ici le dieu des philosophes par opposition au dieu des religions eet des croyants).
Mais est ce à dire que la mathématique et son discours sur l'infini, n'a rien à voir avec D-ieu ? évidemment non.... ne serait ce que parce que tout a "à voir" avec D-ieu, mais cette observation n'aide pas vraiment...
l'infini quantitatif n'est pas l'Infini "nom de " ou "attribut de " D-ieu, mais le fait qu'il soit possible de raisonner et de s'interroger sur l'infini en mathématiques est bel et bien une "preuve", ou un "signe" , que D-ieu est présent dans la pensée comme condition de possiblité de toute évaluation absolue (non relative à la "culture", au temps et au lieu).
Et d'ailleurs l'infini quantitatif s'introduit dans l'Infini philosophique dès les écrits de Spinoza : car comment interpréter l'infinité des attributs de la substance ou des modes, autrement que comme un infini numérique ?
Or, c'est ici le lieu de souligner un grave problème soulevé par nos recherches récentes sur les "entiers infinis", ou "non limités". De tels entiers existent dans les théories dites "non standard", mais ici nous avons suivi une autre voie pour les aborder, motivée d'ailleurs par notre engagement contre la tentation-Badiou.
Celui ci voit en effet dans la mathématique, outre une Pensée "absolue", rien de moins que ce que l'on appelle depuis Aristote l'ontologie, à savoir la théorie de l'Etre en tant qu'être. Et l'ontologie-mathématique, c'est pour lui la théorie des ensembles axiomatisée par Zermelo-Fraenkel, comme théorie de "ce qui est", alors que les topoi ne sont pour lui que de nature logique, théorie des mondes possibles. Et c'est d'ailleurs pour "marquer au fer rouge" notre opposition à Badiou et à l'ontologie que nous avons pris comme pseudo ici même : "topos". Selon nous, les topoi (pluriel de "topos", bien qu'on dise souvent "la théorie des topos") SONT la fondation des mathématiques, et ils permettent d'aller au delà de la pensée ensembliste : au delà de l'Etre, vers l'Un.
Or ceci nous conduit à destituer la théorie des ensembles comme "fondation des nombres" : selon nous, les Nombres (Idées divines) sont premiers, les ensembles viennent après. Et nous observons d'ailleurs que tous les axiomes des théories des ensembles font subtilement appel aux nombres (par exemple dans ZF le "nombre deux" est nécessaire pour parler d'une paire d' ensembles dans certains axiomes) , qui doivent donc "précéder logiquement et métaphysiquement" les ensembles.
La mathématique a le mérite de "solidifier" la pensée et le discours sur l'infini : est dit "fini" un ensemble équipollent à (en bijection avec) un nombre entier , et donc "infini" un ensemble qui ne peut pas faire l'objet d'une telle bijection. La cardinalité d'un ensemble étant défini comme sa "classe d'équipollence", un ensemble fini aura un cardinal fini, qui sera un nombre entier : son nombre d'éléments. Ceci veut dire qu'il est possible d'établir une bijection entre cet ensemble et un "ordinal fini" à savoir un ensemble : { 1,2,...,n}.
Un ensemble infini sera tel qu'il est impossible de touver une telle bijection : c'est donc une définition négative, mais on peut montrer qu'elle est équivalente à cette propriété : un ensemble est infini si et seulement s' il est possible d'établir une bijection entre lui même et une de ses parties propres (une partie propre est une partie d'un ensemble qui n'est pas vide et qui diffère de l'ensemble lui même).
Seulement, c'est ici que surgissent les problèmes évoqués plus haut...
Tant que nous sommes dans le domaine des entiers standard, tout va bien : tout entier est fini, donc un ensemble est dit fini s'il est équipollent à un entier (s'il a comme nombre d'éléments un entier n). Le premier cardinal "infini" est Aleph zéro, le cardinal de N, et il n'est évidemment pas un entier....
Par contre nous avons considéré que l'on peut parler d'entiers non limités, et nous en avons trouvé quelques formulations, à partir du théorème fondamental de l'arithmétique qui affirme que tout entier a une décomposition unique en facteurs premiers.
Notre idée, dans ce type de recherches, est de tout fonder (en ce qui concerne les nombres) sur les nombres premiers : nombres entiers (par le théorème fondamental), puis les autres nombres qui peuvent être dérivés de N par les constructions classiques .
Un entier "non limité" est ainsi le produit de tous les nombres premiers (en nombre infini). Nous pouvons en trouver de "plus grands" en prenant des exposants plus grands que 1 dans cette formule; par exemple nous pouvons donner à chacun des nombres premiers comme exposant : le produit de tous les nombres premiers... et ainsi de suite, jusqu' à un nombre "infini" d'échelons d'exposants.
seulement ceci nous entraîne dans plusieurs difficultés : quel est cet "infini" du nombre des échelons ? car maintenant nous avons plusieurs "infinis" qui ne sont pas tous égaux. Et d'autre part, si nous pouvons parler d'entiers qui sont "infinis", ou "non limités", alors il n'est plus vrai de dire qu'un ensemble équipollent à un entier est "fini".
Il nous faut de toutes façons absolument confronter nos recherches informelles actuelles, qui sont loin d'en être au stade d'une "théorie", même d'une "protothéorie", avec les autres constructions de nombres "non limités", à savoir les nombres hyperréels.
Le livre à lire dans ce domaine pour commencer est celui de Goldblatt qui est ici :
La construction des hyperréels est aussi expliquée sur ce wiki :
http://en.wikipedia.org/wiki/Hyperreal_number
http://en.wikipedia.org/wiki/Ultraproduct
Voir aussi cet article de Benci :
http://www.dm.unipi.it/~dinasso/papers/15.pdf
Or j'extrais du livre de Goldblatt ces informations (pages 56-57) sur les hyperentiers (hyperintegers ou hypernaturals) :
L'extension non standard *N de N est un ensemble dense ordonné de *N-galaxies (qui sont des copies de Z) tel qu'il n'y a pas de plus petite ou de plus grande galaxie.
Une galaxie , pour un entier "non limité" K , est une copie de Z, à savoir l'ensemble des nombres de la forme : K + n ou K - n, n parcourant l'ensemble N des entiers naturels. Si K est un entier naturel, sa "galaxie" est N, qui n'est donc qu'une galaxie particulière dans un ensemble ordonné infini de galaxies. (oui mais quel infini ? peut on dire infini ? ou indéfini ?)
L'ensemble des nombres premiers possède lui aussi une extension *P, consistant en les hyperentiers qui n'ont qu'une décomposition triviale dans *N.
Tout nombre hypernaturel a un facteur "hyperpemier"; deux nombres hypernaturels sont égaux s'ils ont exactement les mêmes facteurs de la forme pn , avec p hyperpremier et n hypernaturel.
Un nombre hypernaturel est divisible par tout nombre entier standard si et seulement s'il est divisible par pn pour tout p premier standard et tout n entier standard.
 votre commentaire
votre commentaire
-
Par topos le 21 Novembre 2009 à 17:13
Reprenons l'expression du nombre que nous avons appelé le MONSTRE et appliquons lui les notations de Conway et Knuth pour simplifier son écriture.
Ce nombre,dans sa décomposition "développée" en facteurs premiers, possède comme facteurs TOUS les nombres premiers (à l'échelon un donc) et ensuite, aux échelons supérieurs qui contiennent les exposants, une infinité d'échelons, et à chaque échelon, TOUS les nombres premiers.
Bien sûr, ceci n'a pas de sens pour les mathématiciens, sauf formel, puisque ces produits divergent; nous avons décidé de confondre ce "nombre" avec les séries qui "à l'infini", convergent vers lui; une telle série est celle qui à l'étape n acommeforme développée : comme facteurs premiers (échelon un) les n premiers nombres premiers; n échelons d'exposants; et à chaque échelon, de nouveau le produit des n premiers nombres premiers.
Or, appelons Pn le produit des n premiers nombres premiers.
Selon la notation de Conway, le nombre à l'étape n de la suite ci-dessus peut s'écrire :
Pn → n → 2
ou, dans la notation de Knuth : Pn ↑↑ n
Soit une tour de n étages :
Pn puissance Pn puissance ... Pn (n fois)
Cette suite peut sembler s'élever assez vite vers le "ciel" des très grands nombres : 2, 6 ^6 , 30 ^30 ^30, ....
et pourtant les nouvelles notations dont nous disposons nous mettent entre les mains des "vaisseaux de navigation" qui , comparés à cette suite poussive, prennent des allures de jet supersonique face à une vieille 2 chevaux.
Car jusqu'ici nous nous contentons d'ajouter UN nombre premier, et UN échelon ! C'est bien, et nous serons rendus au bout "à la fin" (qui n'arrivera jamais).
Mais pouquoi se contenter de la modeste "tour" à deux flèches, qui n'est jamais que l'opération qui suit l'exponentiation ? et surtout pourquoi ne pas "diagonaliser", comme dans le procédé des nombres d'Ackerman ?
Voici une nouvelle suite bien plus "rapide" (le mot est faible), on procède en deux temps :
-d'abord pourquoi se contenter de n'ajouter qu'un seul nombre premier à chaque fois ? choisissons plutôt d'indexer les facteurs premeirs retenus sur la suite elle même, et pour cela imaginons que nous ayions atteint à l'étape n un nombre Sn .
A l'étape (n+1) on prendra les Sn premiers nombres "premiers" et on fera leur produit, que nous noterons : Kn .
Ensuite, deuxième temps, au lieu de se limiter à une banale tour, on indexe le tout , et on prend pour Sn+1 :
Sn+1 = Kn → Kn → Kn
(notation de Conway, voir : http://www.blogg.org/blog-30140-billet-notations_de_knuth_et_conway_pour_les_tres_grands_nombres_entiers-1109408.html )
Essayez de vous représenter ce que cela fait rien qu'en prenant pour premier terme de la suite Sn le nombre : 6^6 !
Nous identifierons le MONSTRE avec cette suite Sn .
 votre commentaire
votre commentaire
-
Par topos le 19 Novembre 2009 à 18:06
La mathesis fait mentir la sagesse paulinienne : il n'est plus vrai que la lettre tue et l'esprit vivifie, et l'on pourrait même dire que la lettre (ou plutôt la notation, le diagramme) EST l'esprit lui même se frayant une voie pour "souffler où il veut"...mais aussi où il peut.
Certes une notation mathématique nouvelle n'est pas un nouveau concept mathématique : on pourrait toujours écrire le nouveau (l'esprit qui souffle où il veut) dans les anciennes notations....sauf quand on ne peut pas !
C'est à la suite de la lecture inopinée du passage d'un livre prodigieux, "Ramsey theory", que je me suis intéressé aux fonctions ackermaniennes et à leur hiérarchie, parce qu'elles sont accompagnées d'une nouvelle notation pour les très grands nombres, et sont donc susceptibles d'apporter des éclaircissements à propos de ce que j'appelle le MONSTRE, à savoir un nombre qui "formalise" la preuve d'Anselme de l'existence de Dieu comme maximum, "ce dont un plus grand ne peut être pensé".
Ce livre extraordinaire sur la théorie de Ramsey est accessible sur Google :
on y parle de la hiérarchie d'Ackerman en paragraphe 2.7 page 60 : "Eeeeenormous upper bounds".
C'est un livre captivant mais difficile, je l'ai en ma possession depuis environ 15 ans et je ne l'ai toujours pas exploré en entier, il est vrai que les traités de mathématiques, surtout quand ils sont ardus comme celui là, ne se lisent pas à la manière des romans.
Mais on peut trouver un court article , écrit par deux des auteurs du livre, Ronald Graham et Joel Spencer, qui livrent en peu de mots l'esprit philosophique de la théorie de Ramsey, qui est une confirmation des analyses de Bergson sur le "désordre et les deux ordres" : le désordre absolu est impossible, tout ensemble assez grand de nombres ou de points possède des régularités et des symétries étonnantes , voir :
http://www.math.ucsd.edu/~sbutler/ron/90_06_ramsey_theory.pdf
La fonction d'Ackermann (datant de 1928 il me semble) est obtenue par un procédé de diagonalisation d'une hiérarchie de fonctions généralisant les opérations élémentaires de multiplication et exponentiation, qui ne sont que les étages les plus bas d'une tour prodigieuse (babélienne?) : cette hiérarchie de fonctions, croissant de plus en plus vite, commence avec f1(x) = 2x , suivie de l'exponentielle f2(x) = 2x , puis par la fonction f3 appelée TOWER (tour) qui consiste en une tour de 2 puissance 2 puissance 2.... x fois.
On passe ensuite à la fonction f4 appelée par nos auteurs WOW parce qu'on ne peut que pousser un cri de surprise : WOW devant l'immensité des nombres qu'elle met déjà en jeu (rien qu'au bout de 4 itérations). La suite infinie est définie par une double induction, voir la page 60 du livre, et la fonction d'Ackermann croît plus vite que TOUTE fonction de la suite, aussi bien que de toute fonction primitivement récursive, car elle est obtenue par diagonalisation , c'est à dire que l'on ne prend plus un indice fixe fi (x), mais on fait varier l'indice avec x :
Ackermann (x) = fx(x)
Voir là dessus un lien plus complet car plus restreint au sujet des fonctions ackermaniennes :
http://en.wikipedia.org/wiki/Ackermann_function
il y a aussi des fonctions "Ackermann inverse", qui croissent avec une lenteur prodigieuse, voir liens à la fin de celui ci dessus.
Mais ce lien cite, et c'est là que je veux surtout en venir, car je pense toujours au MONSTRE, jour et nuit, des notations aptes à faciliter la compréhension des nombres extrêmement grands.
Ceux ci forment, avec les grands cardinaux (qui sont autre chose, là nous nous restreignons aux entiers, bornés donc par l'infini dénombrable qui est le cardinal infini le plus bas, Aleph zéro de Cantor) un sujet de réflexions passionnées pour pas mal de mordus, dont votre serviteur... voir le site de Munafo, qui avoue carrément y avoir consacré une grande partie de sa vie, comme le capitaine Achab à la poursuite de la baleine blanche dans Moby dick de Melville :
http://www.mrob.com/pub/math/largenum.html
Les notations (inventées au 20 ème siècle) pour les très grands nombres sont des généralisations, sur le mode de la hiérarchie des fonctions d'Ackermann, des opérations élémentaires, qui sont :
l'opération "successeur" (qui correspond à un des axiomes de Peano pour les nombres entiers) : à un nombre entier a on associe son successeur a + 1
l'addition : on obtient à partir de l'entier a le nouvel entier a + b en itérant b fois l'opération "successeur" : a + 1 + 1 + 1...+ 1 (on ajoute 1 b fois)
la multiplication : pour obtenir le produit a x b à partir de l'entier a on itère b fois l'opération précédente d'addition, c'est à dire qu'on ajoute b fois l'entier a à lui même:
a x b = a + a +... + a (b fois)
l'exponentiation : là encore on itère b fois l'opération précédente (multiplication) pour obtenir a à la puissance b :
ab = a x a x a x .... x a (b fois)
à partir de là nous quittons le domaine des opérations courantes pour entrer dans celui des "tours d'exposants", qui peuvent encore à la rigueur s'exposer dans le langage de l'exponentiation, mais où de nouvelles notations rendent de grands services de simplification et de clarification. Le procédé de récurrence sera toujours le même : on passe d'une opération à la suivante, dans une hiérarchie ackermanienne qui n'a pas de fin, en itérant celle ci b fois.
Notation de Knuth avec des flèches verticales orientées vers le haut (up-arrows)
ainsi l'opération suivant l'exponentiation correspond elle à la fonction d'Ackermann TOWER = f3 . Elle peut s'écrire d'abord dans la notation en flèches verticales inventée par Knuth: on notera d'abord, dans cette notation nouvelle qui est comme un nouveau langage, l'exponentiation avec une flèche verticale vers le haut :
ab = a
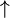 b
bl'opération suivant l'exponentiation , consistant à itérer celle ci, sera notée naturellement avec deux flèches vers le haut :
a
 b = a
b = a 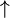 a ...
a ... 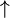 ...
...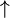 a (b fois)
a (b fois)Cela consiste en une "tour" de a puissance a puissance a etc... , ceci b fois.

Attnetion, l'opération d'exponentiation n'est pas associative, ni commutative d'ailleurs : elle est "associative à droite" (right-associative), c'est à dire qu'il faut partir de la droite et remonter vers la gauche.
exemple : 3 puissance 3 puissance 2 = 3^3^2 est égal à : 3 ^(3 ^2 ) = 3 ^9 (3 puissance 9) et non à : (3^3) ^2 = 27 ^2 ( 27 puissance 2) .
On procèdera ainsi de suite avec trois flèches, quatre, n , etc... :
 = a
= a  ...
...  a (b fois)
a (b fois)Comme cela devient trop compliqué à partir de 4 ou 5 on notera :
 l'opération consistant en n flèches orientées vers le haut.
l'opération consistant en n flèches orientées vers le haut.a
 b = a ...
b = a ... 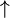 ...
...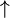 a (avec n flèches)
a (avec n flèches)Voir ce lien pour des explications complètes : http://en.wikipedia.org/wiki/Knuth%27s_up-arrow_notation
(on lira notamment le paragraphe "Writing out up-arrow notation in terms of powers" pour avoir une idée de l'énormité des nombres mis en jeu à partir de trois ou quatre flèches...et que l'on pense que l'on peut augmenter le nombre des flèches à l'infini !).
Notation de Conway avec des flèches horizontales en chaîne :
C'est une notation équivalente, plus pratique dans certains cas, moins dans d'autres ; mais en tout cas elle est plus facile avec les outils (assez restreitns) que Blogg met à ma disposition, ce sera donc celle que j'utiliserai surtout à l'avenir ... elle est expliquée sur ce lien :
http://en.wikipedia.org/wiki/Conway_chained_arrow_notation
Ici l'exponentiation est aussi notée par une flèche (comme chez Knuth) mais horizontale (comme un morphisme dans une catégorie, ou une application entre ensembles, mais attention, ici les flèches ne se composent pas entre elles !):
ab = a
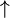 b (Knuth) = a → b (Conway)
b (Knuth) = a → b (Conway)Comment traduit on les 2 flèches, 3 flèches, n flèches de Knuth ? pas avec deux, trois, ou n flèches horizontales, car cela serait trop difficile (surtout sur Internet et sur Blogg notamment !).
non, le coup de génie de Conway est d'avoir permis à une deuxième flèche de faire son apparition . L'opération "Tower", avec deux flèches, devient dans la notation de Conway :
a
 b = a → b → 2
b = a → b → 2et ainsi de suite, pour trois, quatre, n flèches de Knuth : deux flèches de Conway suffisent :
a
 b = a ...
b = a ... 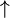 ...
...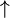 a (avec n flèches) = a → b → n
a (avec n flèches) = a → b → nIncroyablement simple et intelligent, n'est ce pas ?
C'est dans ce genre de situations que l'invention d'une nouvelle notation, en mathématiques, à condition bien sûr qu'elle soit féconde, est beaucoup plus que de simple nature "formelle" : disons que le "contenu" descend avec, s'incarne dans la forme. L'exemple paradigmatique de ceci est la théorie des catégories, où le simple ajout d'une flèche (d'un morphisme) , puis d'un diagramme plus ou moins complexe de flèches, permet de trouver, de créer ( ?) des "essences mathématiques" tout à fait inédites.
Car les flèches de Conway peuvent s'inclure dans des schémas bien plus complexes, qu'il est possible de "calculer" à partir des quatre règles données dans le lien ci dessus, au début.
C'est ainsi (voir le lien) que l'on peut montrer assez vite que :
a→ b → 2 → 2 = a → b → ab
Hyperoperations :
Les deux notations précédentes peuvent se fondre dans le cadre conceptuel des hyperopérations, expliquées dans le lien suivant :
http://en.wikipedia.org/wiki/Hyper_operator
Les opérations appelées précédemment , successeur, addition, multiplication, exponentiation sont respectivement : Hyper0, hyper1, hyper2 et hyper3. En fait Hypern correspond à (n-2) flèches verticales dans la notation de Knuth, on pourra donc noter :
a
 b = a ...
b = a ... 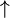 ...
...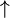 a (avec n flèches) = a → b → n = Hn+2 (a,b)
a (avec n flèches) = a → b → n = Hn+2 (a,b)H4 s'appelle tetration : http://en.wikipedia.org/wiki/Tetration
mais les hyperoperations peuvent prendre d'autres formes.
Encore quelques sites à lire pour ceux que le sujet passionne (ce qui est mon cas) :
http://en.wikipedia.org/wiki/Pentation
http://en.wikipedia.org/wiki/Steinhaus-Moser_notation
http://www-users.cs.york.ac.uk/~susan/cyc/b/big.htm
Dans un article à venir on utilisera ce genre de notations pour simplifier les expressions des séries menant au MONSTRE, c'est à dire au nombre entier "infini" que nous avons défini d'après sa décomposition "développée" en facteurs premiers comme "le plus grand" : un nombre infini d'échelons d'exposants et à chaque échelon tous les nombres premiers, en nombre infini.
 votre commentaire
votre commentaire
-
Par topos le 15 Novembre 2009 à 17:34
Le nombre entier non limité que j'ai appelé le Monstre, et que j'ai défini dans l'article précédent, est, de par sa construction même, tel que l'on ne peut concevoir aucun entier "infini" (ou "non limité") qui soit "plus grand" .
En effet, un tel entier aurait une décomposition en facteurs premiers , qui devrait, à un "échelon" au moins, comporter des facteurs premiers qui ne figureraient pas dans celle du Monstre : or c'est impossible, car le Monstre est justement construit de façon à avoir à chaque échelon TOUS les facteurs premiers (en nombre infini).
Il s'agit donc de l'entier infini tel qu'aucun autre plus grand ne puisse être pensé.
Ceci rappelle l'argument d'Anselme de Cantorbéry prouvant l'existence de Dieu comme maximum, tel que rien de plus grand ne puisse être pensé.
Disons qu'il s'agit de la même pensée, mais "rabaissée" du niveau métaphysique ineffable où se plaçait Anselme au niveau arithmétique.
C'est pourquoi j'appelle le Monstre : le Père.
On peut le penser (comme "maximum") mais pas le "comprendre", à cause de l'infinité du processus de construction, qui est une "infinité d'infinités".
Par contre je vais indiquer ici une "voie unique menant au Père" que j'appelle donc le Fils : il s'agit d'un geste très banal en mathématiques, ainsi par exemple je rappelle la construction des nombres réels par les "coupures de Dedekind" : un réel est défini au moyen de deux séries de rationnels convergeant vers une même limite, l'une en croissant , l'autre en décroissant de façon monotone.
Voici brièvement cette construction : on prend comme premier nombre le nombre 2, soit le premier "nombre premier". On le prend à la puissance 1 puisque comme c'est la première étape il n'y a pas d'exposant à l'échelon supérieur. Cette première étape correspond à l'échelon 1, celui où il n'y a pas d'exposants.
Comme deuxième tape on ajoute le facteur premier suivant, soit 3, au niveau horizontal, et l'on ajoute un échelon , où l'on mettra les mêmes facteurs, soit 2 et 3, comme exposants de chacun des facteurs de l'échelon un : on aura donc le nombre : (2 ^ (2.3)) . (3 ^(2.3)), ce qui fait :
6^6 ( 6 à la puissance 6).
Ensuite on ajoutera le facteur premier suivant , soit 5, à tous les échelons déjà remplis (l'échelon zéro et l'échelon un) et on ajoute un échelon, où l'on mettra les mêmes facteurs : on aura donc à l'échelon un : 2 . 3 . 5 = 30; chacun de ces trois facteurs aura à son tour comme exposants (à l'échelon deux donc) 2.3.5; et chacun de ces trois facteurs de l'échelon deux aura lui même comme exposants 2.3.5, à l'échelon trois donc. Ce serait à la rigueur encore possible de l'écrire sous forme mathématique avec des signes ^ représentant l'exponentiation et des parenthèses, mais cela serait déjà assez inextricable...
Et ainsi de suite : à chaque tape on ajoute un facteur premier, et un échelon. Ainsi à la n-ième étape on aura n échelons remplis ainsi :
à l'échelon un : n facteurs qui sont les n premiers nombres premiers, soit p1 = 2, p2 = 3, .... pn
à l'échelon deux : chacun des n facteurs précédents a comme exposants les même n nombres : p1 , p2 , .... pn
à l'échelon trois : chacun des n facteurs a à son tour comme exposants : p1 , p2 , .... pn .... et ainsi de suite jusqu'à l'échelon n
Et l'on passe de l'étape n à l'étape n + 1 en ajoutant un échelon d'exposants, et en ajoutant à chaque échelon un facteurs premiers, le suivant dans la liste des nombres premiers, soit le (n +1 ) ème nombre
premier.
en procédant ainsi on est sûr de n'oublier aucun facteur premier, puisqu'on les prend tous dans l'ordre de la liste par ordre croissant, et de remplir tous les échelons : certes , à une étape n, on peut avoir des entiers plus grands que l'entier défini ci dessus et ayant le même nombre d'échelons, il suffit par exemple de prendre les mêmes facteurs premiers pour les échelons de un à (n-1) et à l'échelon n de prendre plus de facteurs premiers; mais "à l'infini", tous les échelons seront remplis de tous les nombres premiers.
Par construction cette suite tend donc , en itérant le processus à l'infini, vers le Monstre, c'est à dire le Père.
Aussi j'appelle cette suite le Fils : c'est un "geste spirituel" fréquent de confondre la suite (infinie) avec sa limite, ce qui dans mon langage se dit : le Fils est l'unique voie menant au Père, et le Fils se confond (est UN) avec le Père.
Ainsi, dans la construction par "coupures de Dedekind" que j'évoquais plus haut, on peut montrer que les deux suites convergent vers une limite commune, mais pas expliciter cette limite : on peut dire que le nombre réel qui est cette limite "se confond" avec les deux suites.
Bien entendu, la différence est ici que la suite diverge : mais nous considérons que nous avons le droit de parler de nombres infinis.... pour parler autrement, nous pensons les suites en suspendant notre jugement sur le fait qu'elles convergent ou non: il s'agit d'une "épochè".
Car la suite du Fils, que je viens de définir, est rigoureusement "pensable", puisqu'à tous les niveaux on reste dans le "fini" (même si cela devient rapidement inextricable).
Nous avons le Père, le Fils, où est l'Esprit (Saint) ?
c'est tout simplement l'Esprit (l'Intellect) de tout homme (ou être pensant) réfléchissant sur ce mathème, faisant l'effort de méditer, de se laisser illuminer par Lui.
Je considère que ce "mathème" de la Trinité vaut bien ceux de Lacan.
Il permet de rationaliser, de rendre rigoureusement (mathématiquement) pensables certaines notions métaphysiques qui sans cela courraient le risque de rester "mystiques" ou ineffables.
 votre commentaire
votre commentaire
-
Par topos le 13 Novembre 2009 à 16:26
Petit rappel d'un article récent : nous nous sommes laissés aller à "raisonner" sur des nombres entiers infiniment grands, ou "non limités", dans l'esprit des théories non standard...
dans la formule donnant pour tout entier sa décomposition (unique à l'ordre prés) en facteurs premiers (sous la forme d'un produit infini ) :
n= ∏ i pi ki (l'index i est celui de la série infinie des nombres premiers, donnée ici :
il suffit de ne plus se restreindre aux nombres "classiques" pour lesquels l'exposant ki est nul sauf pour un nombre "fini" de pi . On envisagera donc des nombres "infiniment grands" , ayant une infinité de facteurs premiers, qui seront donc des produits vraiment infinis. On pourra par exemple parler rationnellement du nombre produit de TOUS les nombres premiers :
P = ∏ i pi (l'exposant ki est égal à 1 pour tous les pi ).
En fait nous appellerons dorénavant ce nombre infini, que nous venons de définir (ou plutôt dont nous affirmons que nous venons de le définir, car je sais que les puristes se gausseront ) : P0
pour des raisons que nous allons maintenant exposer.
La décomposition de tout entier n en facteurs premiers peut s'écrire sous forme dde fonction : P → N associant à chaque nombre premier son exposant ; seulement, comme cet exposant est à son tour un entier, il possède à son tour une décomposition en facteurs premiers, d'où une forme développée pouvant s'écrire comme une suite emboîtée de fonctions :
P → ( P → ... ( P → N)
dans la plupart des cas, cette forme développée s'arrêtera au bout de trois ou quatre "étages", mais théoriquement elle peut s'itérer à l'infini (attention, l'exponentiation n'étant pas asociative, les flèches ne se composent pas, d'où l'importance des parenthèses).
Nous notons P0 parce qu'on en reste à l'échelon zéro (pas d'exposant au niveau 1). Mais on peut définir un P1 en donnant à chaque nombre premier un exposant égal à P0.
Et ainsi de suite, à l'infini... on aura donc une suite infinie et vertigineuse d'infinis dont chacun, au niveau n, se définira en fonction de celui de niveau (n-1) par :
Pn = ∏ i ( pi ^ Pn-1)
Notons : P∞ = P le nombre obtenu (idéalement) en itérant ce processus à l'infini. On peut aussi le considérer comme la suite infinie elle même. Nous l'appelons le MONSTRE.
Par définition ce nombre "infiniment infini" n'aura aucun nombre infini "au dessus de lui", à cause de la nature même du processus de cosntruction : nous prenons, à chaque échelon d'exponentiation, tous les nombres premiers.
Il me semble qu'il s'agit de l'aleph zéro de Cantor, ou l'infini dénombrable, mais ramassé en une formule..
il possède des propriétés très spéciales, puisque multiplié par lui même un nombre indéfini de fois il reste égal à lui même...
En tout cas tous ces nombres entiers infinis peuvent bien s'additionner, se multiplier, se comparer dans des relations d'ordre...
 votre commentaire
votre commentaire Suivre le flux RSS des articles de cette rubrique
Suivre le flux RSS des articles de cette rubrique Suivre le flux RSS des commentaires de cette rubrique
Suivre le flux RSS des commentaires de cette rubrique
puisque le salut est en nous, n'est il pas assuré que l'armée des esprits débouche dans l'éternité, pourvu que nous ayons soin de maintenir à la notion d'éternité sa stricte signification d'immanence radicale ?